Un señor de Atenas - La red
geométrica de los templos y centros de culto de Grecia -
¿Instigadores Euclides o Platón? - Edificaciones en sección
áurea - Emplazamientos sobre puntos de circulo - El sistema
geométrico sobrepasa los límites de Grecia - Investigadores
rusos descubren ordenaciones geométricas a escala global -
Lo que dicen los sioux - Cultos nacidos hoy - Entre los
bantú de África - Mas'udi nunca oyó hablar de Zimbabwe - "No
de mano humana" - Zimbabwe medida y estudiada - Los extraños
pájaros de Zimbabwe - ¿Erigida con arreglo al sistema de
Sirio? (p.191)
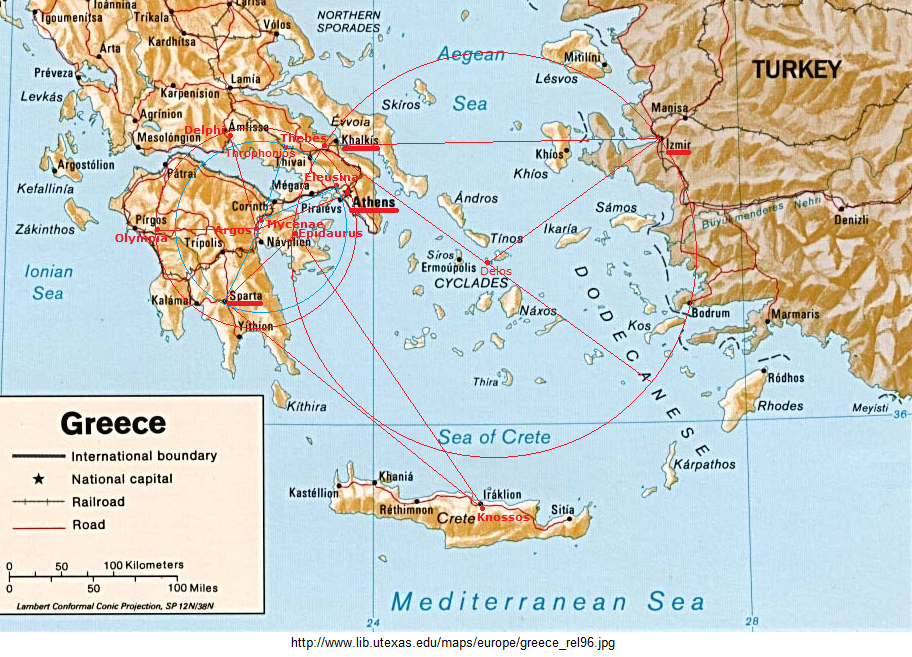
[5.1. Las distancias
entre los templos y santuarios en Grecia]
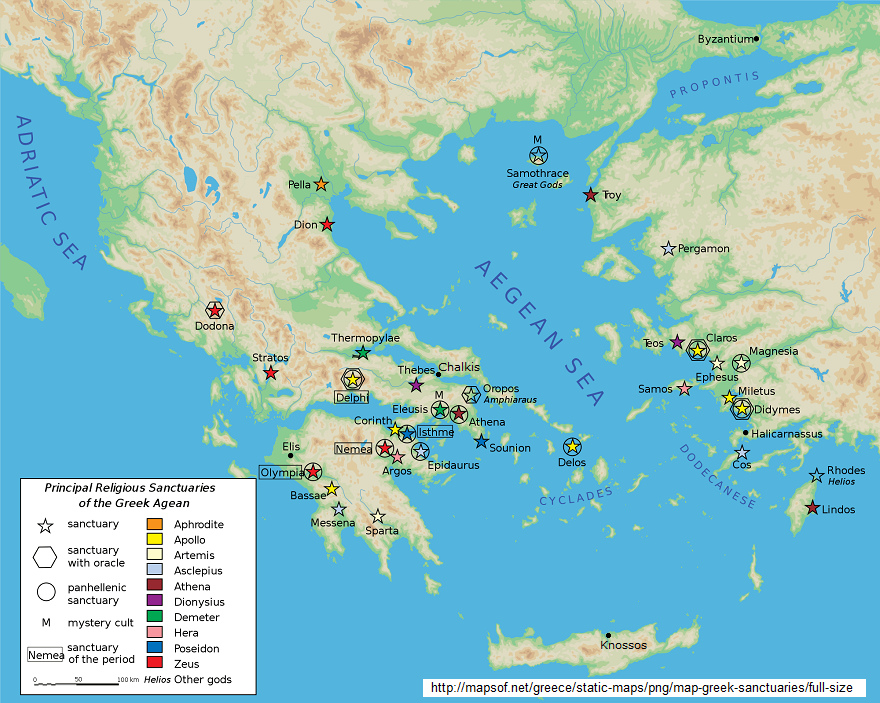
Mapa de Grecia con los santuarios
Ocurrió hace algunos años, en Atenas. Mientras me hallaba
celebrando una conferencia de prensa me fijé en un señor que
no hacía preguntas, pero tomaba notas con gran interés. A la
salida se dirigió hacia mí y me preguntó, con exquisitos
modales, si sabía yo que todos los templos griegos, incluso
aquellos cuya construcción data de los tiempos mitológicos,
están dispuestos de tal manera que guardan relaciones
geométricas exactas entre sí.
Debí sonreír con algo de ironía, pues aquel señor insistió
asegurándome ser cierto lo que me estaba explicando.
Como no ignoro que a los oyentes les agrada hacerme un (p.191)
favor con una información sobre indicios susceptibles de dar
lugar a nuevos desarrollos especulativos, decidí escucharle.
No, le dije, no había oído hablar nunca de eso,y además no me
parecía lógico, pues no imaginaba que los "antiguos griegos"
poseyeran conocimientos geodésicos tales como para incluir sus
edificaciones de templos en un esquema geométrico; por otra
parte, los templos distan entre sí, en muchos casos, cientos
de kilómetros, y así se lo dije. Entre ellos hay montañas que
imposibilitan todo alineamiento de las obras, y era de
considerar que incluso en las islas menores existían templos,
los cuales no habrían sido visibles desde la costa ni en los
días más despejados. No, resumí mi punto de vista, yo no podía
concebir qué interés habría movido a los constructores para
establecer los templos y santuarios de acuerdo con unas
proporciones geométricas cualesquiera.
Mi interlocutor se encogió de hombros, como pidiendo perdón
por haber abusado de mi tiempo, y se fue después de manifestar
que le había decepcionado con mi escepticismo... No tardé en
olvidarle. Pero su imagen volvió a presentarse ante mí cuando
llegaron a mi mesa dos trabajos científicos que confirmaban
las aseveraciones de aquel señor griego. Una de esas
publicaciones era del doctor Theophanis M. Manias
(nota 37: Manias, Dr.
Theophanis, M.: The invisible harmony of the ancient Greek
world and the apocryphal geometry of the Greeks - the
geometric geodetic triangulation of the ancient Hellenic
space; Edition of National Institution; Atenas 1969),
brigadier del arma aérea griega, y la otra del profesor doctor
Fritz Rogowski,
(nota 38: Rogowski, Prof. Dr.
Fritz: Tennen und Steinkreise in Griechenland; Mitteilungen
der Technischen Universität Carolo-Wilhelmina zu
Braunschweig; Herausgegeben von Prof. Dr. Edgar R. Rosen; en
colaboración con la Liga Universitaria de Braunschweig, año
VIII/2/1973)
de la universidad técnica Carolo-Wilhelmina de Braunschweig.
Ambos autores demuestran sin lugar a dudas que TODOS los
lugares de culto, por ejemplo las sedes de los oráculos, así
como todos los templos antiguos, están dispuestos conforme a
un "modelo geométrico-geodésico de triangulación". Al leer
estos artículos me acordé de mi interlocutor en Atenas. Me
gustaría disculparme por mi frívolo escepticismo, pero
desconozco hasta el nombre de aquel señor. Bien, espero que mi
inteligente interlocutor se entere de mi conversión cuando
este libro sea publicado por la editorial Notos de Atenas.
|

Euclides, retrado [1]

Platón, retrato [2]
|
|
¿Ideas de Euclides?
De por sí, el hecho de que los templos fuesen erigidos con
arreglo a principios geométricos no tendría por qué ser un
"prodigio", puesto que la antigua Grecia produjo a uno de los
mayores matemáticos de todos los tiempos: Euclides, que vivió
hacia fines del siglo IV a.d.C., dio lecciones en la
universidad (p.192)
platónica de Alejandría y abarcó en sus quince libros toda la
gama de las matemáticas y, en particular, de la geometría.
¿Fue Euclides el autor de la idea de situar los templos tal
como están emplazados?
¿Qué hizo y cuánto supo
Platón?
Euclides fue contemporáneo del filósofo Platón, que también
destacó por sus actividades políticas. Platón había acudido a
Mégara para sentarse a los pies de Euclides y escuchar sus
lecciones. ¿Tal vez Platón se sintió fascinado por las ideas
de su colega? ¿Recordó los conocimientos adquiridos cuando,
una vez investido de funciones políticas, hubo de votar
proyectos y adjudicaciones de obras? ¿Fue así como se ordenó a
los arquitectos que edificasen los templos en disposición
triangular?
La idea es sugestiva, pero errónea, ¡pues la mayoría de los
templos y santuarios se erigieron mucho ANTES de la época de
Euclides!
Sin embargo, parece que Platón debió saber algo acerca de la
misteriosa red geométrica de los monumentos de la Antigüedad
griega, pues menciona en los capítulos séptimo y octavo de su
diálogo "Timeo" (Timaios) toda una serie de relaciones
geométricas. Platón, el maestro del diálogo de claridad
cristalina, tenía una gran opinión de la geometría. Aún hoy,
muchos tratados geométricos citan en su prólogo esta frase de
Platón:
<Ningún ignorante de la geometría debe hablar en la
asamblea. La geometría es la ciencia del Ser eterno.>
Es muy posible que Euclides le hablase a Platón de los
misterios geométricos YA EXISTENTES, que sin duda debió haber
observado. Lo cual implica que Euclides pudo contar con un
antiquísimo saber geométrico plasmado en piedra en los templos
y lugares sagrados de la antigua Hellas. Por eso dice también
el doctor Manias: "Toda la geometría euclidiana emana de un
antiquísimo códice religioso-científico." (nota 37: Mantas,
cit.)
La "sección áurea" expresada
en piedra
Todo el mundo sabe qué es la sección áurea. Ya Euclides
(p.193)
escribió al respecto. Pero antes de exponer algunos ejemplos
sorprendentes de relaciones geométricas entre lugares sagrados
erigidos de acuerdo con las proporciones de la "regla áurea"
vamos a recordar la definición de la misma, que he tomado de
un manual escolar (nota 39: Grether, Edwald: Theorieheft
Planemateria, 2ª parte, sin fecha) de mi hija:
SE LLAMA SECCIÓN ÁUREA DE UN SEGMENTO "AB" AL SEGMENTO "AE"
DETERMINADO POR UN PUNTO "E" TAL QUE LA RAZÓN DE "AB "A "AE"
SEA IDÉNTICA A LA DE "AE" A "EB":







 6
6