Geometrisches
Zeichnen
|
Das Geometrische
Zeichnen im MNG Basel
(Mathematisch-naturwissenschaftliches Gymnasium
Basel) fand nur für 13-Jährige statt und war eines
meiner Lieblingsfächer, damals noch unter meinem
alten Nachnamen "Schulz" (Details über den
Psychoterror im MNG gegen den Namen "Schulz" habe
ich hier
zusammengefasst). In diesem "Geometrischen
Zeichnen" wurden Naturphänomene und Naturgesetze
des Grossen Geistes dargestellt, ohne dass über
den Grossen Geist je etwas unterrichtet wurde. Die
Verbindung von Zeichnung und geistigem Leben wurde
konsequent unterlassen. Manchmal wurde auch eine
mathematische Aufgabe dargestellt und somit auch
in zeichnerischer Form "verarbeitet", oder es
wurden alltägliche Sachen graphisch verarbeitet.
Wenn die Lehrperson eine gute Lehrperson ist, kann
das geometrische Zeichnen mit seiner präzisen
Arbeit und einem vorzeigbaren, guten Resultat eine
geistige Schulung auch für viele andere
Lebensbereiche sein. Es ist ein Jammer, dass das
Fach "Geometrisches Zeichnen" nur ein Jahr lang
gegeben wurde, und dass viele Erwachsene keinen
Zugang zum geometrischen Zeichnen haben.
Die Materialien waren ein pultgrosses Reissbrett
mit cm-Mass und einem Architektenwinkel dran, ein
Zirkel mit der Vorrichtung für einen Tintenfüller,
Kalkpapier, eine Rasierklinge, und ein
Tintenfüllerset mit verschiedenen Spitzen und
Farben. Des Weiteren hatten wir noch ein
Kurvenlineal und Schreibschablonen. Heute wird das
alles am Computer gemacht. Ob der Vorgang derselbe
ist mag ich zu bezweifeln, aber er ist sicher
ähnlich. Am Computer erspart man sich das
Wegkratzen von Fehlern mitder Rasierklinge. Manche
haben sich dann Löcher in das Papier gekratzt. Das
passiert am Compi nicht mehr.
|

 Geometrisches
Zeichnen
im MNG Basel 1977-1978, Titelblatt auf dem grossen
Briefumschlag (Couvert), worin die Zeichnungen
aufbewahrt wurden Geometrisches
Zeichnen
im MNG Basel 1977-1978, Titelblatt auf dem grossen
Briefumschlag (Couvert), worin die Zeichnungen
aufbewahrt wurden
|
Ich habe diese
geometrischen Zeichnungen bis 2008 aufbewahrt,
denn präzise Darstellungen sind für mich ein
wesentliches Lebenselement für die
Entscheidungsfindung und für die Urteilsfindung
im Leben, also für die analytische Arbeit. Diese
Zeichnungen sind in diesem Sinn ein grosses
Symbol für den Arbeitsvorgang der
Problemstellung und der Problemlösung durch
Genauigkeit.
Präzise und
logisch arbeiten und logisch denken, das
verkörpert das geometrische Zeichnen. Der Grosse
Geist spricht hier seine irdischen Gesetze durch
seine Gesten mit Lineal und vor allem mit dem
Zirkel. Manchen Menschen täte es wirklich gut,
sich logisch-geometrisch besser zu schulen, um
Manipulationen im Leben zu erkennen und um von
Manipulationen wegzukommen, sich von
Unwahrheiten loszulösen und sich neue geistige
Freiheiten zu erarbeiten. Es gab aber sicher
auch einige Schüler, die das geometrische
Zeichnen "nicht wichtig" fanden und sich allein
auf die Algebra konzentrierten. Wieso sollte man
viel "machen" für ein Fach, das es nur ein Jahr
gab...
Bei der Auswanderung nach Süd-"Amerika" im Jahre
2008 habe ich dann die Zeichnungen nicht mehr
mitnehmen können, sondern habe sie eingescannt.
Da wegen der immer grösser werdenden Webseite
ein grösseres Interesse an meiner Biographie
besteht, seien sie hier präsentiert.
|
 Figur
1: Strichübung mit Bleistift, 13.5.1977 Figur
1: Strichübung mit Bleistift, 13.5.1977 |

 Figur
2: Strichübung mit Tinte, 13.5.1977 Figur
2: Strichübung mit Tinte, 13.5.1977
|
1+2.
Die erste Zeichnung, eine "Strichübung"
Nun, mit irgendeiner simplen Figur muss man ja
anfangen, um die Jugendlichen an eine
zeichnerische Präzision zu gewöhnen. Bei uns war
die erste Figur ein Rechteck mit vielen gekreuzten
Quadraten.
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
|
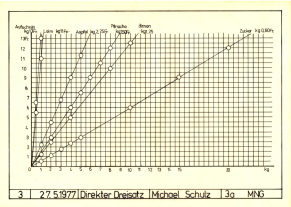
 Figur
3: Direkter Dreisatz, Schema, 27.5.1977 Figur
3: Direkter Dreisatz, Schema, 27.5.1977
|
3. Darstellung
eines direkten Dreisatz
Die Grafik des einfachen Dreisatzes zeigt noch
die Ungeschicklichkeit mit der Schablone.
Hilfslinien waren im Unterricht beim schweizer
Terror-Lehrer Walter Fankhauser verboten, und so
stellen die Zahlenreihen eher Kurven dar, was
von mir gar nicht so gewollt war. Nun gab es
sicher einige Schüler, die hatten zu Hause ein
Reissbrett und hatten schon Übung mit
Schablonen. Bei denen waren die Zahlenreihen
wirklich schon "Reihen". Die zeichnerische
Aufgabe an sich ist eine Sisyphusarbeit mit
vielen kleinen Quadraten und Kreisen, eine fast
unsinnig und stumpfsinnig anmutende
Präzisionsarbeit.
So weit ich es
in Erinnerung habe, durften die Schüler das
Thema frei wählen, zu dem der Dreisatz
ausgeführt wurde. Der Dreisatz zeigt in meinem
Fall alltägliche Produkte (v.a.
Lebensmittelpreise) mit den Preisen von 1977:
Aufschnitt 13 Franken pro kg, Leim 11 Fr./kg,
Äpfel 2,25 Fr./kg, Pfirsiche 1,50 Fr./kg, Birnen
1,25 Fr./kg, Zucker 0,60 Fr./kg.
|

Figur 4: Wunderblume, 3.6.1977
|
4. Eine
Wunderblume
Die Aufgabe mit der "Wunderblume" war, mit dem
Zirkel einen Kreis in 12 Abschnitte zu
unterteilen und dann alle Punkte miteinander zu
verbinden. Das Resultat war diese Rosette. Wenn
man die Blüten in der Natur oder die
Kirchenfenster anschaut, so verwundert es, wieso
wir nicht noch mehr Rosetten gezeichnet haben.
Es sind alles wunderschöne Mandalas, wunderbare
Wunderblumen.
|
 Figur 5: Autorennbahn, 19.8.1977
Figur 5: Autorennbahn, 19.8.1977
|
5. Eine
Autorennbahn
Bei der Figur "Autorennbahn" kam es zu ersten
Anwendung des "Kurvenlineals". Man hätte die
Figur auch "Wegenetz" nennen können, aber in
einer Bubenklasse mit Jugendlichen macht die
Bezeichnung "Autorennbahn" mehr Emotionen frei.
Wie man sieht, bereitete mir die Anwendung eines
"Kurvenlineals" noch einige Mühe. Ich hatte das
vorher noch nie gesehen.
Es war eigenartig, dass die geistig armseligen
MNG-Schüler gerne Autorennen schauten und die
Sekunden und die Bruchteile von Sekunden genau
beobachteten. Eigentlich wollte ich damals schon
in eine geistig andere Welt...
|

 Figur 6: Kreisdiagramm, 23.9.1977
Figur 6: Kreisdiagramm, 23.9.1977 |
6. Ein
Kreisdiagramm
Das Kreisdiagramm über die "Areale der Schweiz"
war eine erste statistische Aufgabe und zeigt
die territoriale Aufteilung der Schweiz von
1977. Die Schüler hatten da schon mit der
Schablone "schreiben gelernt" und die Buchstaben
kamen nun einigermassen auf "eine Reihe". Die
Knacknuss war, Zahlen genau in kleine Kreise zu
setzen.
Als produktive Flächen der Schweiz wurden im Jahre
1977 gezählt:
1. Äcker, Wiesen mit 10.800 qkm, 26,2%, mit einer
Kreisfläche von 94,32º
2. Weiden mit 10.660 qkm, 25,8%, mit einer
Kreisfläche von 92,88º
3. Wald mit 9800 qkm, 23,7%, mit einer Kreisfläche
von 85,32º
Als unproduktive Flächen der Schweiz wurden im
Jahre 1977 gezählt:
1. Siedlungen mit 1050 qkm, 2,5%, mit einer
Kreisfläche von 9º
2. Seen mit 1390 qkm, 3,4%, mit einer Kreisfläche
von 12,24º
3. Übriges (Berge, Halden, Sümpfe etc.) mit 7580
qkm, 18,4%, mit einer Kreisfläche von 66,24º
|
|
Nun, so
"produktiv" sind die Äcker heute leider nicht
mehr, weil die Böden oft mit Pestiziden
verseucht sind, und weil viele Böden unter
Mineralienarmut leiden, weil die Böden kaum noch
überschwemmt werden. Früchte und Gemüse sind
also oft vergiftet und geben kaum noch
Mineralien her. Das wäre dann wieder eine andere
Statistik...
|

Figur 7: Indirekter Dreisatz, 21.10.1977
|
7.
Darstellung eines indirekten Dreisatz
Der indirekte Dreisatz ist hier mit Arbeitstagen
von Arbeitergruppen im Strassenbau dargestellt.
Die zeichnerische Aufgabe an sich ist - wie beim
einfachen Dreisatz schon - auch hier wieder eine
Sisyphusarbeit mit vielen kleinen Quadraten und
Kreisen, eine fast unsinnig und stumpfsinnig
anmutende Präzisionsarbeit, dieses Mal aber noch
verbunden mit Kurvenlineal.
|
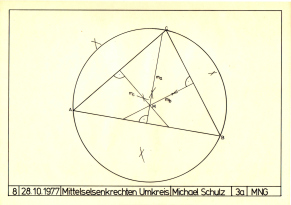
 Figur 8: Mittelsenkrechte mit Umkreis
Figur 8: Mittelsenkrechte mit Umkreis
|
8. Die drei
Mittelsenkrechten und der Umkreis
Es wurde ein
Dreieck gezeichnet, dann mit dem Zirkel die
Mitten der Seiten bestimmt und darauf die
Senkrechten gezeichnet. Die Mittelsenkrechten
ergeben einen Schnittpunkt, der der Mittelpunkt
des "Umkreises" ist, des Kreises, der die
Spitzen des Dreiecks schneidet.
Wie man sieht, ist die Aufgabe gut gelöst. Heute
(2010) werden solche logisch-räumlichen Vorgänge
automatisch von Computerprogrammen wie Corel
Draw ausgeführt.
|
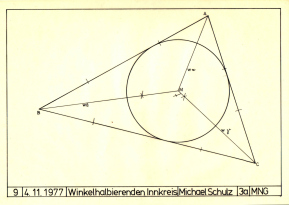
 Figur 9: Winkelhalbierenden mit Inkreis, 4.11.1977
Figur 9: Winkelhalbierenden mit Inkreis, 4.11.1977
|
9. Die drei
Winkelhalbierenden mit dem Inkreis
Zuerst wurde ein Dreieck gezeichnet, dann die
Winkelhalbierenden mit dem Zirkel bestimmt.
Sodann wurden die Winkelhalbierenden gezeichnet,
und der Treffpunkt ist der Mittelpunkt des
"Inkreises", der gemeinsame Kreis, der die drei
Seiten berührt. Solche Figuren kommen in vielen
geometrischen Figuren vor, in Kirchenfenstern,
bei künstlerisch gestalteten Hausfassaden etc.
Wie man sieht,
ist auch diese Aufgabe gut gelöst, bis auf das
falsche Wort "Innkreis". Der Fluss "Inn" im
Engadin war mir scheinbar geläufiger als der
einfache "Inkreis". Heute (2010) werden solche
logisch-räumlichen Vorgänge automatisch von
Computerprogrammen wie Corel Draw ausgeführt.
|

 Figur 10: Die Aussenwinkelhalbierenden und die
Ankreise, 11.11.1977
Figur 10: Die Aussenwinkelhalbierenden und die
Ankreise, 11.11.1977
|
10: Die
drei Aussenwinkelhalbierenden und die drei
Ankreise
Die
Aussenwinkelhalbierenden und die "Ankreise" sind
nach demselben Prinzip gestaltet wie die
"Inkreise", aber ausserhalb des Grund-Dreiecks.
Zuerst wird ein kleines Dreieck gezeichnet,
dessen Schenkel aber sehr verlängert sind. Dann
werden die Winkelhalbierenden gezeichnet, die
ein eigenes Dreieck um das Grund-Dreieck
ergeben. Das Winkelhalbierenden-Dreieck bildet
die Mittelpunkte der Ankreise. Der Radius ist
mit einer Senkrechten auf die Schenkel
ermittelbar.
Der grosse
Zusammenhang zwischen Zeichnung 9 und 10 ist ein
philosophisch-logischer: Mit dem Inkreis und den
Ankreisen ist der Umkehrschluss zeichnerisch
dargestellt. Wenn ein Vorgang passiert, dann ist
auch auf der anderen Seite ein Vorgang möglich,
der mit dem ersten Vorgang i
|

Figur 11: Die Seitenhalbierenden, die
Mittellinien, und der Schwerpunkt bei einem
Dreieck
|
11. Die
Seitenhalbierenden, Mittellinie und Schwerpunkt
Zuerst wurde ein grosses Dreieck gezeichnet,
dann mit dem Zirkel die Seitenmitten bestimmt
und darauf die Verbindung der Mittelpunkte und
den gegenüberliegenden Ecken gezogen. Dies wurde
einige Male nach innen hin wiederholt. Das
Resultat ist eine eigenartige, nach innen
gerichtetes Dreieck-Auge.
Der Schwerpunkt wird mit den Mittellinien und
nicht mit den Winkelhalbierenden bestimmt.
|
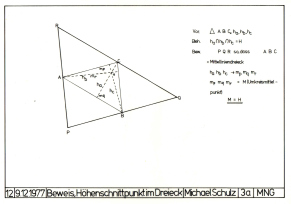
 Figur 12: Der Beweis eines Höhenschnittpunkts im
Dreieck, 9.12.1977
Figur 12: Der Beweis eines Höhenschnittpunkts im
Dreieck, 9.12.1977
|
12: Der
Beweis eines Höhenschnittpunkts im Dreieck
In der
vorliegenden Zeichnung wurden die Mittelpunkte
der Seiten verbunden, was das innere Dreieck
ergab (wie in Zeichnung 11). Dann wurden die
"Höhen" des kleineren Dreiecks eingezeichnet
(die Linie, die senkrecht auf der Seite steht
und die gegenüberliegende Ecke schneidet). Diese
"Höhen" des kleinen Dreiecks haben einen
Schnittpunkt.
Es wurde hier der geometrische Beweis geführt,
dass der Höhenschnittpunkt des kleinen Dreiecks
der Schnittpunkt der Mittelsenkrechten und somit
der Mittelpunkt des Umkreises des grossen
Dreiecks sei (wie in Zeichnung 8). Solche
abstrakten Beweisführungen sind jedoch nicht
sehr verständlich, wenn alles in einer einzigen
Figur gezeichnet ist.
Hier begann sich ganz konkret, die Denkweise der
"MNG-ler" von der Denkweise anderer Jugendlicher
zu unterscheiden, und das war ganz bewusst so
manipuliert. Solche "Codes" sind meines
Erachtens absolut destruktiv und spalten die
Gesellschaft in überflüssiger Weise auf. Die
MNG-ler sollten also ihren eigenen "Code" haben,
der sich dann an der ETH, in der Justiz
als "Detektiv" und in den Geheimdiensten der
Justiz fortsetzt, ein grausamer Menschenschlag
mit vielen "Codes", aber ohne jede Ahnung über
Menschen.
|

 Figur 13: Besondere Punkte und Linien im
Dreieck, 22.12.1977
Figur 13: Besondere Punkte und Linien im
Dreieck, 22.12.1977 |
13: Besondere
Punkte und Linien im Dreieck
In
diesem geometrischen Kunstwerk sind die
Zeichnungen 8 bis 12 alle in einer Figur
vereint. Ein Scan in A3 war mir nicht
möglich, deswegen musste ich den Scan
zusammensetzen, so dass im Mittelbereich
ein paar leicht versetzte Linien
entstanden. Man sieht hier
-- gelb: die Winkelhalbierenden mit dem
Inkreismittelpunkt und dem Inkreis
-- blau: die Mittelsenkrechten, der
Umkreismittelpunkt und der Umkreis
-- grün: die Seitenhalbierenden, der
Schwerpunkt und die Mittellinien
-- rot: die Höhen und der
Höhenschnittpunkt
-- schwarz: die drei
Aussenwinkelhalbierenden, das Dreieck
der Aussenwinkelhalbierenden und die
Ankreise
-- blau und fett: die Eulersche Gerade,
die gerade Linie zwischen
Umkreismittelpunkt, Schwerpunkt und
Höhenschnittpunkt)
-- rot und fett: der Feuerbachsche
Kreis, der alle Ankreise und den Inkreis
schneidet.
|
An dieser grossen Zeichnung sieht man einige
Sachen:
Erstens war
diese grosse Dreieckszeichnung mit all ihren
Elementen der Ausdruck einer grossen geistigen
Fähigkeit, aus verschiedenen Elementen eine
grosse Lösung herbeizuführen (Eulersche Gerade,
Feuerbachsche Kreis). Präzise Arbeitsweise war
mir eigentlich eine Leidenschaft. Einige meiner
MNG-Kameraden sind an dieser grossen Aufgabe
gescheitert.
Und zweitens sieht man hier bereits, dass sich
die geometrische Zeichnerei von der allgemeinen
Lebenspraxis bereits etwas entfernt hat und zu
einem Tüftler-Gebiet wird. Die MNG-ler sollten
sich alle als "Tüftler" fühlen, Tüftler für
grosse Problembereiche, wo Lösungen gesucht
wurden, so wie die "Eulersche Gerade" etc.
|
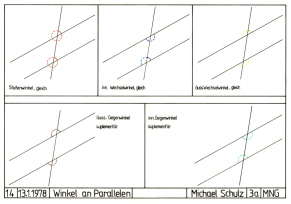
 Figur 14: Winkel an Parallelen, 13.1.1978
Figur 14: Winkel an Parallelen, 13.1.1978
|
14. Winkel
an Parallelen
Hier sind in
einfacher Art und Weise Stufenwinkel,
Wechselwinkel und Gegenwinkel dargestellt. Uns
Schülern wurde aber nie gesagt, für welche
Berufe man dieses Wissen um innere und äussere
Gegenwinkel und Innenwinkel schlussendlich
braucht. Es fehlte im Unterricht völlig die
Vision des späteren Anwendungsgebietes im Beruf.
Die verschiedenen Codewörter für die Winkel
waren wieder eine Spezialität für sich. Im
"normalen" Leben braucht man solche
Bezeichnungen eigentlich nie...
|
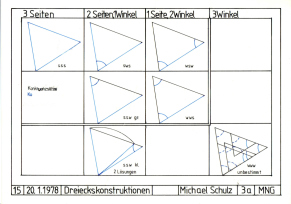
 Figur 15: Dreieckskonstruktionen, 20.1.1978
Figur 15: Dreieckskonstruktionen, 20.1.1978
|
Zeichnung
15: Dreieckskonstruktionen
Die Übersicht zeigt, nach welchen Kriterien
Dreiecke konstruiert werden können:
-- einmal sind drei Seitenlängen vorgegeben (Code:
sss)
-- ein anderes Mal sind zwei Seitenlängen und ein
Winkel vorgegeben (Code: sws)
-- ein weiteres Mal sind eine Seitenlänge und zwei
Winkel vorgegeben (Code: wsw)
-- oder dann sind drei Winkel vorgegeben (Code:
www).
Bei der Vorgabe
von zwei Seitenlängen und einem Winkel gibt es
zwei Lösungsmöglichkeiten, das Dreieck zu
konstruieren. Bei drei vorgegebenen Winkeln gibt
es keine Lösung, weil das Dreieck beliebig gross
oder klein präsentiert werden kann. Diese
logischen Schlussfolgerungen waren wiederum
geistig formgebend.
|
Man sieht gleichzeitig wieder den "MNG-Code"
der Geometrie (sss, sws, wsw, www). Dieses
Code-Denken war die Vorbereitung auf ETH und
Geheimdienste. Am Ende sollten die Menschen
einfach gar nicht mehr reden, sondern nur noch
Codes schnattern. Das waren dann die "MNG-ler",
die auf ihr Code-Wissen stolz waren, soziologisch
und psychologisch aber oft bis heute (2010) eine
quasi 0-Bildung haben und somit
soziologisch-psychologisch absolut dumm bleiben.
Da fehlt allgemein etwas im Lehrplan der
Gymnasien, wobei eben auch das Geometrische
Zeichnen eine geistige Schulung ist, wenn es nicht
zu abstrakt unterrichtet wird.
|
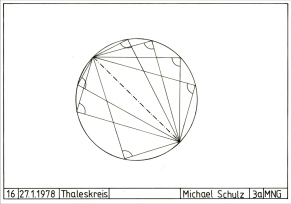
 Figur 16: Thaleskreis, 27.1.1978
Figur 16: Thaleskreis, 27.1.1978
|
16.
Thaleskreis
Der Grieche
Thales soll die Gesetzmässigkeit gefunden haben,
dass innerhalb eines Halbkreises alle
Dreieckswinkel 90 Grad sind.
Es wurde ein Kreis gemalt, eine gestrichelte
Mittellinie, und dann willkürlich Linien von den
Endpunkten der Mittellinie zum Kreis. So ergab
sich immer ein Winkel von jeweils 90 Grad.
|

 Figur 17: Steigung und Gefälle, 24.2.1978
Figur 17: Steigung und Gefälle, 24.2.1978
|
17.
Steigung und Gefälle
In dieser
Darstellung wurden die Steigung im Winkelmass in
Prozent ausgerechnet, verglichen an der Länge
der rechten Linie des entstehenden Dreiecks.
Also wird eine Steigung mit einem 45 Grad-Winkel
als 100% bezeichnet, weil die Basislinie und die
rechte Linie des entstehenden Dreiecks dann
gleich lang sind. Man sollte diese 100%-Steigung
eigentlich rot eintragen. Die anderen Werte sind
jeweils angegeben, und die rechten Seitenlinien
sind bei den drei steilsten Steigungen
unvollständig. Das bräuchte ein grösseres
Papier...
Diese Aufgabe war absolut realitätsbezogen, und
im Nachhinein fragt es sich, wieso diese Aufgabe
nicht schon früher kam.
|
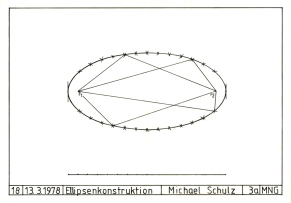
 Figur 18: Ellipsenkonstruktion, 13.3.1978
Figur 18: Ellipsenkonstruktion, 13.3.1978
|
18.
Ellipsenkonstruktion
Diese
Konstruktion war nicht so schwer, wie sie
aussieht, man musste nur wissen wie: Zuerst
wurden zwei Punkte "F1" und "F2" festgesetzt
("Brennpunkte"), Darauf wurde eine zweite Linie
(unten) definiert, die Gesamtstrecke der beiden
Dreiecksschenkel. der Hilfsdreiecke. Die
"Gesamtlinie" (unten) wurde dann regelmässig
unterteilt, und dann wird der Zirkeljeweils in
zwei sich ergänzenden Strecken eingestellt und
so die Zirkellinien geschnitten, so dass die
vielen Schnittpunkte entstehen (sieht ja aus wie
die Nähpunkte einer Narbe etc.). Am Ende
wurden die Punkte mit dem Kurvenlineal
verbunden.
Der Abstand "hinter" den Brennpunkten ist die
Differenz der Strecke zwischen den Brennpunkten
und der Gesamtlinie.
Geistig war diese Konstruktion eine weitere
Entwicklung, eine schwierige Aufgabe mit
Disziplin und Präzision zu lösen. Ausserdem
sieht man hier zum ersten Mal das Phänomen der
optischen Täuschung durch die Dreieckspunkte,
die optisch die Ellipse beeinträchtigen.
|
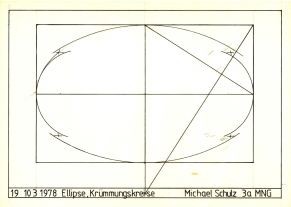
 Figur 19: Ellipse mit Krümmungskreisen, 10.3.1978
Figur 19: Ellipse mit Krümmungskreisen, 10.3.1978
|
19. Ellipse
mit Krümmungskreisen
"Krümmungskreise"
sind Kreise, die die Ellipse an den
Scheitelpunkten berühren. Hier sind die beiden
Krümmungskreise ansatzweise dargestellt. Die
Ellipse fehlt.
An dieser Konstruktion sieht man, dass die
MNG-ler in Basel schon das abstrakte Denken
entwickelt hatten, gewisse Sachen einfach
wegzulassen.
Für mich persönlich ging hier eines meiner
besten Fächer zu Ende, das geometrische
Zeichnen. Stattdessen wurde am MNG Basel nun in
den folgenden Klassenstufen das "abstrakte
Denken" in Codes und Zeichen weiter
"perfektioniert", was mir absolut zuwiderlief,
denn so weltfremd wollte ich gar nicht leben...
|
|